Maths at Sacred Heart Primary School
There are daily mathematics lessons for all children. Fluency, problem solving and reasoning are key elements evident in every lesson throughout the school. Children learn through a clear progression of mental and written methods with the aim of developing a deepened understanding of mathematical strands. The following are essential components which teachers embed in their everyday teaching to ensure the delivery of maths is of a high standard.
-
- Coherence
Children are exposed to opportunities to connect new ideas to concepts that have already been understood, and ensuring that, once understood and mastered, new ideas are used again in next steps of learning, all steps being small steps.
- Coherence
-
- Representation and Structure
Representations used in lessons expose the mathematical structure being taught, the aim being that students can do the maths without recourse to the representation. Concrete, pictorial and abstract representations are varied to ensure children fully understand maths concepts.
- Representation and Structure
-
- Mathematical Thinking
Ideas are to be understood deeply. To enable this, mathematical elements must not merely be passively received but must be explored thoroughly by the student: thought about, reasoned with and discussed with others.
- Mathematical Thinking
-
- Fluency
Children should be able to recall facts quick and efficiently. With flexibility, children should competently move between different contexts, procedures and representations of mathematics.
- Fluency
-
- Variation
Varying the way a concept is initially presented to students, by giving examples that display a concept as well as those that don’t display it. Also, carefully varying practice questions so that mechanical repetition is avoided, and thinking is encouraged. Reasoning and problem solving should address and eliminate misconceptions.
- Variation
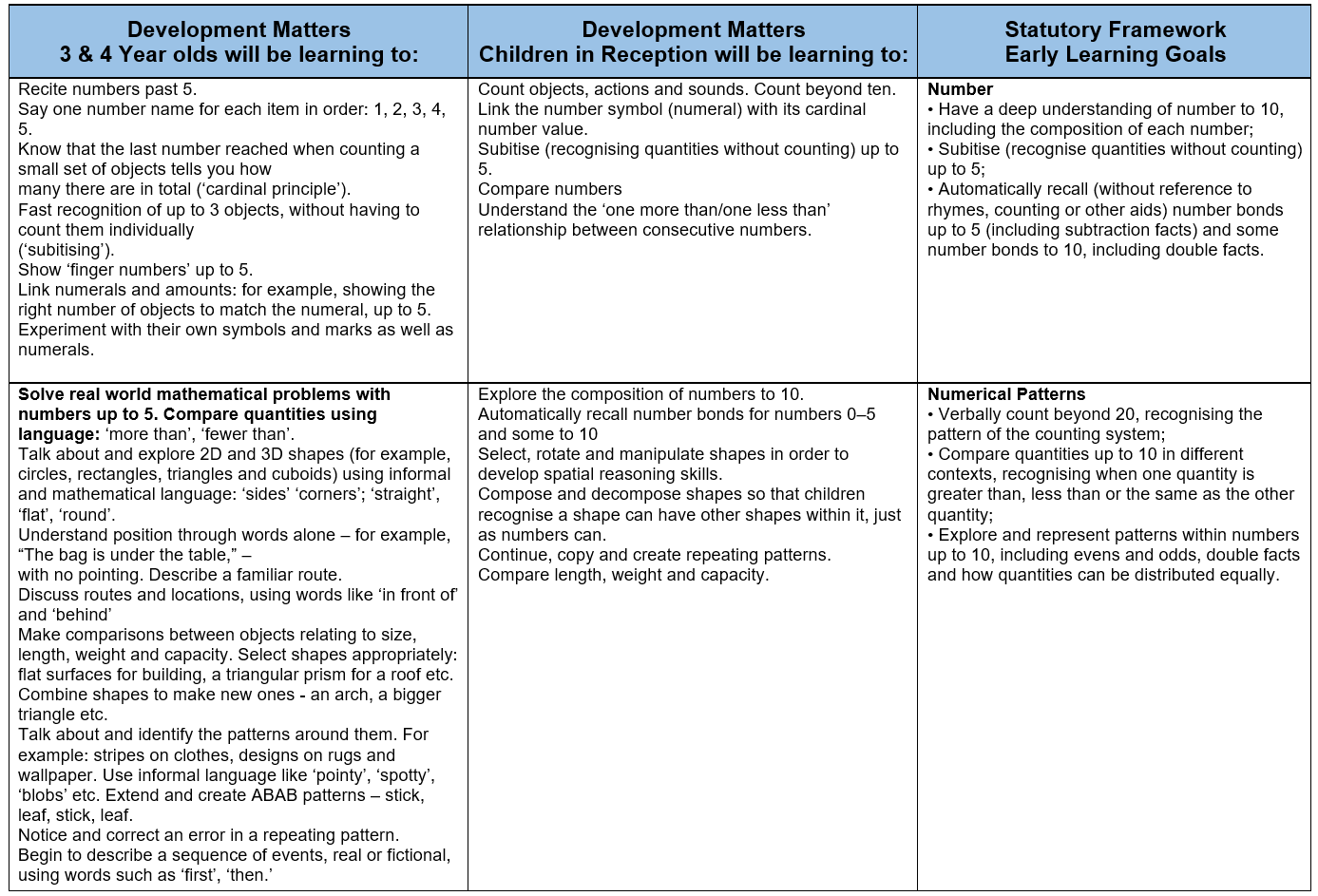
EYFS Educational Programme – Maths
Developing a strong grounding in number is essential so that all children develop the necessary building blocks to excel mathematically. Children should be able to count confidently, develop a deep understanding of the numbers to 10, the relationships between them and the patterns within those numbers. By providing frequent and varied opportunities to build and apply this understanding – such as using manipulatives, including small pebbles and tens frames for organising counting – children will develop a secure base of knowledge and vocabulary from which mastery of mathematics is built. In addition, it is important that the curriculum includes rich opportunities for children to develop their spatial reasoning skills across all areas of mathematics including shape, space and measures. It is important that children develop positive attitudes and interests in mathematics, look for patterns and relationships, spot connections, ‘have a go’, talk to adults and peers about what they notice and not be afraid to make mistakes.
For further information on how calculations are taught at Sacred Heart Primary School, please click on the below image.
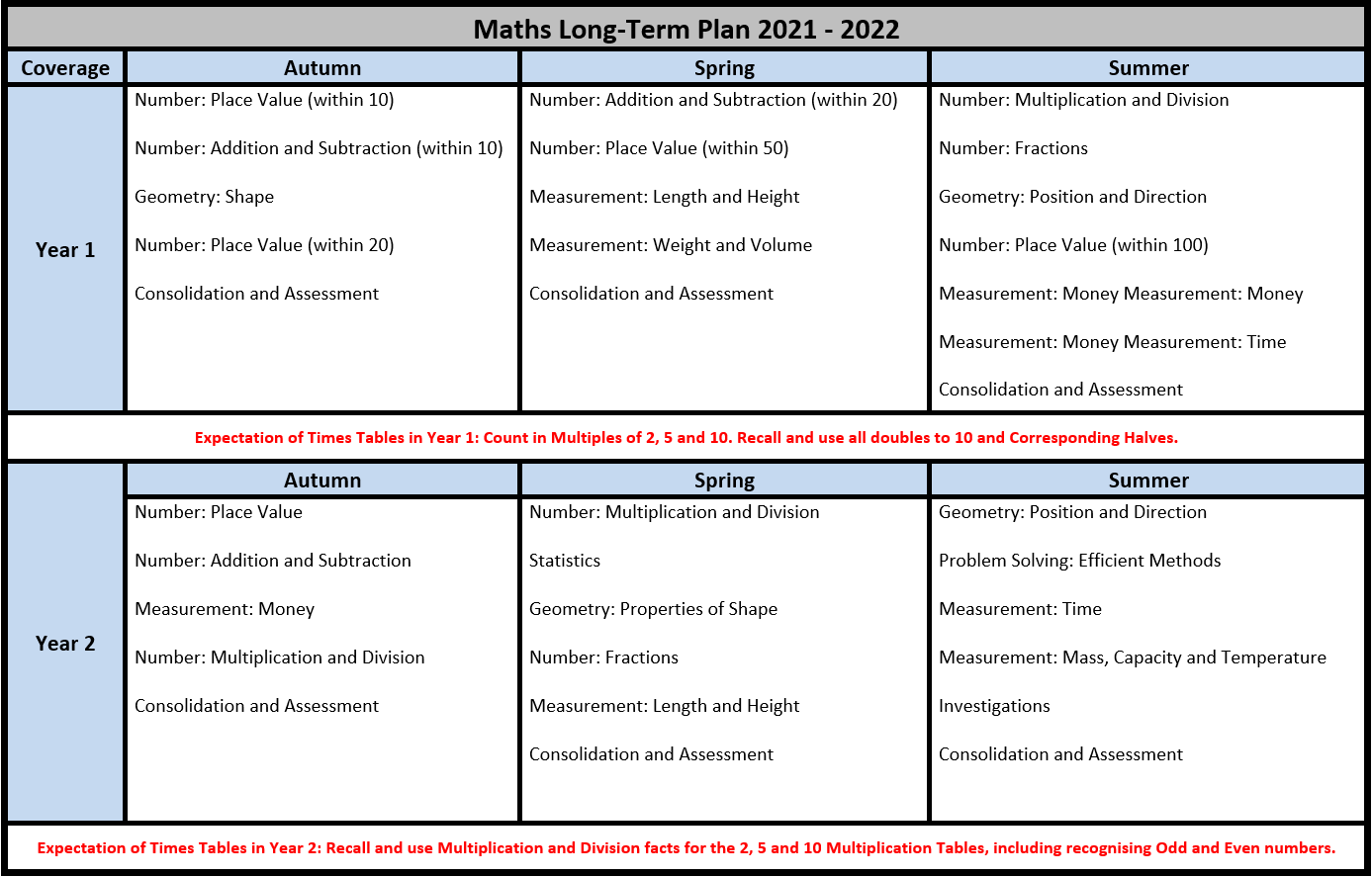
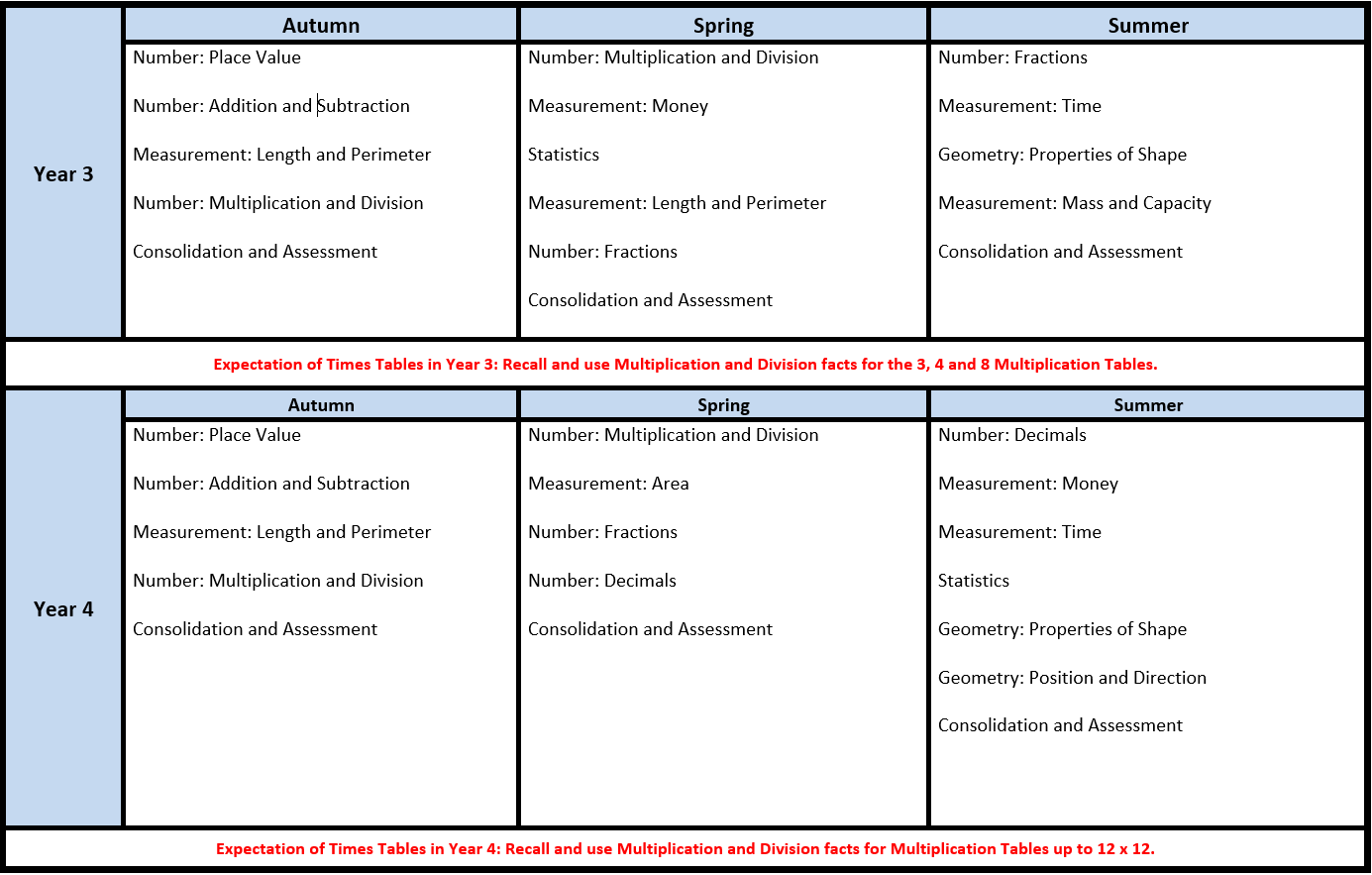
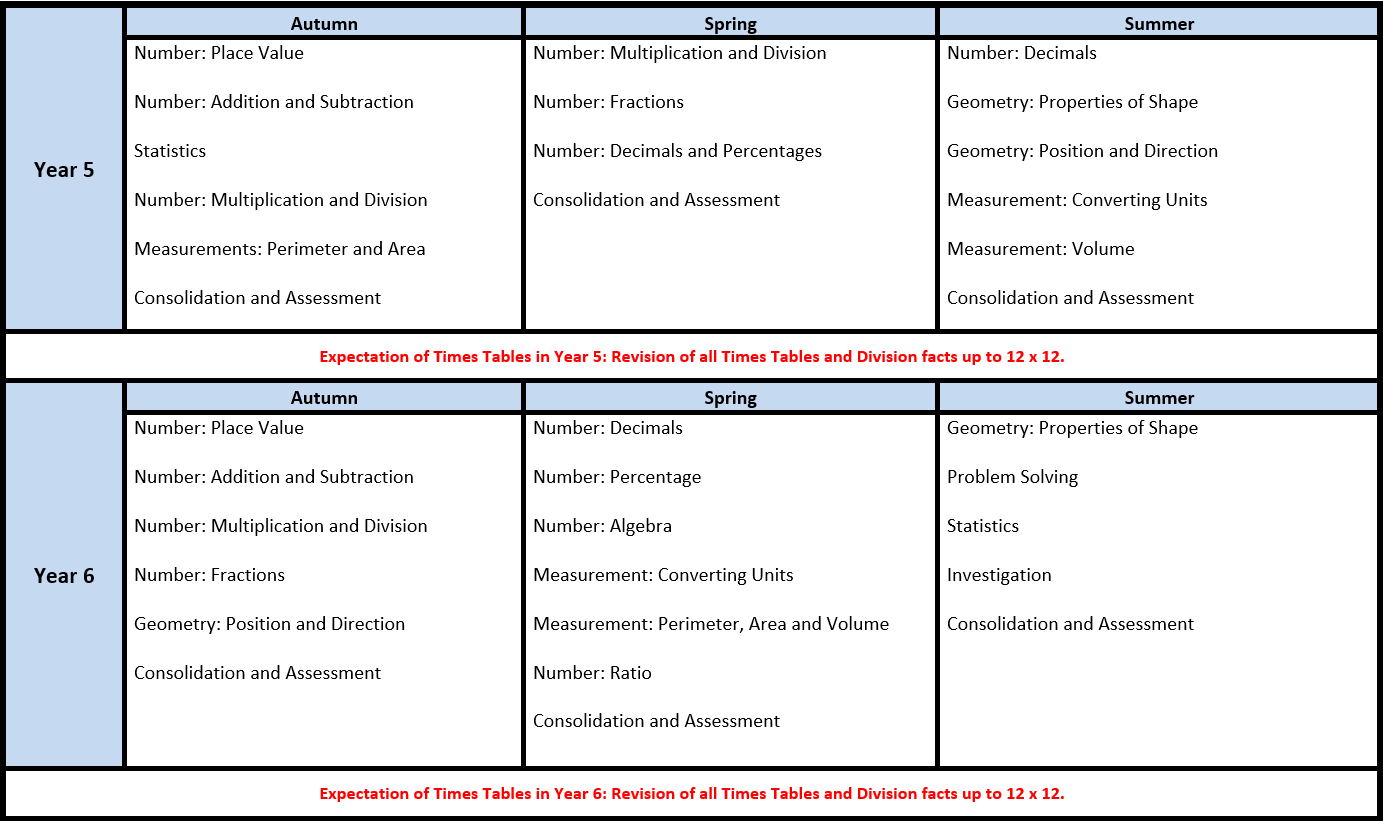
National Curriculum – Purpose of Study
Mathematics is a creative and highly inter-connected discipline that has been developed over centuries, providing the solution to some of history’s most intriguing problems. It is essential to everyday life, critical to science, technology and engineering, and necessary for financial literacy and most forms of employment. A high-quality mathematics education therefore provides a foundation for understanding the world, the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject.
National Curriculum – Aims
The National Curriculum for Mathematics Aims to ensure that all Pupils:
- Become Fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.
- Reason Mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language.
- Can Solve Problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.
Mathematics is an interconnected subject in which pupils need to be able to move fluently between representations of mathematical ideas. The programmes of study are, by necessity, organised into apparently distinct domains, but pupils should make rich connections across mathematical ideas to develop fluency, mathematical reasoning and competence in solving increasingly sophisticated problems. They should also apply their mathematical knowledge to science and other subjects.
The expectation is that the majority of pupils will move through the programmes of study at broadly the same pace. However, decisions about when to progress should always be based on the security of pupils’ understanding and their readiness to progress to the next stage. Pupils who grasp concepts rapidly should be challenged through being offered rich and sophisticated problems before any acceleration through new content. Those who are not sufficiently fluent with earlier material should consolidate their understanding, including through additional practice, before moving on.









